NB: The recent release of the F# CTP breaks much of this code. I will update this page as soon as I get a chance, but please be aware that if you copy the code in as-is, it will not work.

I think the best way to appreciate how efficient F# is, especially for numerical analysis, is to show an implementation of a short program. The following is a bare-bones application which computes the basins of attraction for a Newton fixed point iteration which finds the roots of a polynomial in the complex plane. This computation is threaded across all available processors, and is a stand alone (albeit absolutely minimal) Windows application. The entire program is less than 50 lines, a testament to F# with respect to numerics and the .NET framework with respect to the GUI.

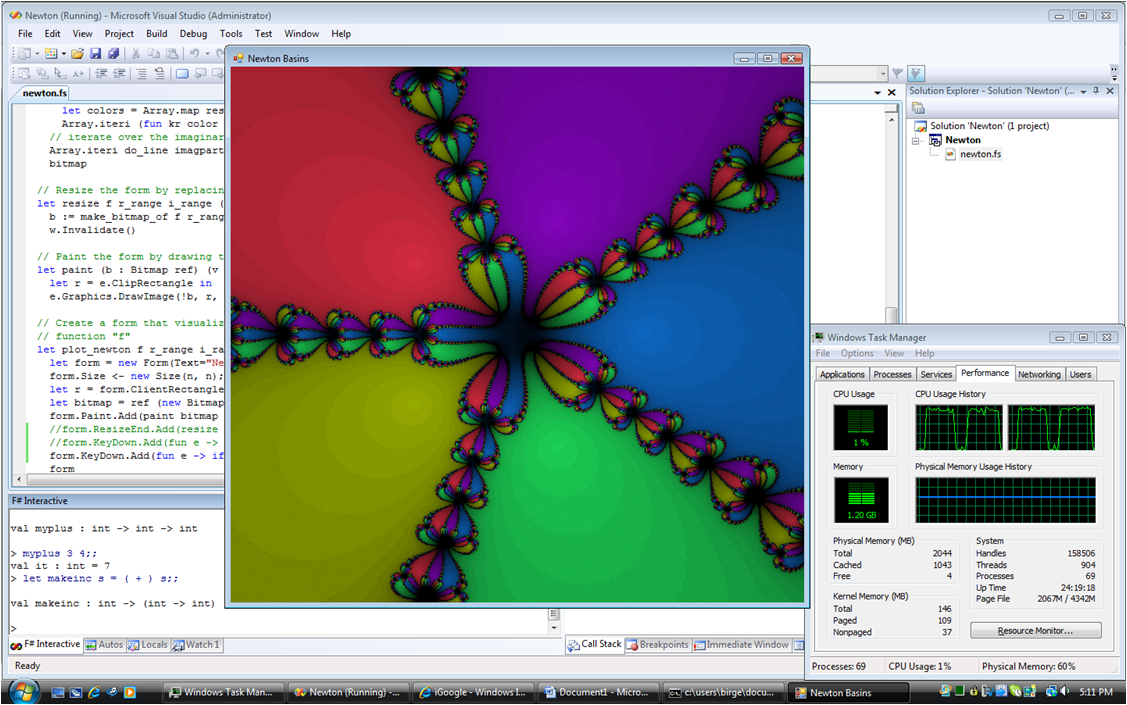
Briefly, Newton’s method is an iterative way to solve for the zeros of nonlinear functions. You start with an initial guess, and based on the local slope of the function, you make a refined guess for the root by following the slope all the way to zero. Unless the function really is a line this guess will be wrong, of course, but hopefully a little more accurate than where you started. If you start close enough to a root, repeated applications of the approximation will end up converging to the correct answer to arbitrary precision. If you start far away from one, however, you could end up at a root far away from your starting point, or you might never converge. It turns out that the map of where you end up as a function of where you start is a fractal, and a rather beautiful one for many equations. Below is a screen shot of the final program. Visible in the task manager is the nearly full usage of both cores of the processor during the render. (Click for a bigger version.)

Screenshot showing the nearly full use of both cores during the render.

The program below will iterate through up to 32 steps of Newton’s method on an arbitrary polynomial, starting at a grid of points in the complex plane. It shades each point based on the location of the final root found, with the hue determined by which root is converged to and with the brightness determined by how many steps were required. I’ll go through most of the functions, explaining each and pointing out how functional programming techniques are used. I do not claim this program is a highly efficient implementation! The main point was to illustrate several aspects of F#. It is however, pretty fast and makes use of multiple threads. In fact, the ease with which this program was parallelized is one of the main points I am trying to illustrate, and is made possible by the immutability of data in F# (and the Flying Frog Numerics library, a review of the which will be the subject of my final post on F#).

Continue reading →

Computer programmers sometimes mistake brevity for elegance, especially when discussing the relative merits of programming languages. Haskel partisans, for example, love to show how one can implement QuickSort in one line of inscrutable gibberish that looks like somebody had an epileptic seizure with the caps lock on. Haskell is a great language, but not because it saves you some typing. If being concise is really all that important, one might as well define a new programming language called ZipC, whose “compiler” is defined as “gunzip -c $1 | gcc”. You’ll get some really concise and “elegant” programs out of that, I’m sure! I’m usually pretty wary of academic languages like Lisp and ML, which often put computer science orthodoxy above usability. I’m just not interested in investing the time to learn a new language just so that I can save some typing and use cute tricks. The time saved is likely to be more than offset by the inefficiency of maintaining competence in multiple special purpose languages.

F#, however, is the first new language in a long time that I’ve felt is worth taking the time to learn. Developed by Microsoft research in England, F# is a functional language with roots in ML. Unlike many academic functional languages, however, F# is a pragmatic mix of imperative object oriented programming and functional constructs. Instead of forcing a paradigm on you, it simply makes several available. It can also leverage the full .NET framework, and is thus just as capable of implementing a GUI as it is an abstract recursive algorithm. It produces code that’s about as fast as C#, and it should only get faster with improvements in its CLR compiler and in .NET’s JIT compiler. A novel aspect of F# (in the context of .NET languages) is that it can be used as an interactive scripting language from within Visual Studio, allowing for interactive data visualization.

After working with it for a month or so, I find it to be a highly productive and expressive language, especially for numerical algorithms. It manages to be concise and high-level while maintaining coherence and readability. Well-written functions in F# are easier to follow and debug, relative to C++ or C#, and there are fewer opportunities for bugs to begin with. More than just cute syntax, it’s a language that actually encourages you to think differently. Programs implemented well in F# are a closer representation of the underlying concept and thinking, and are less obscured with with mundane details. Perhaps the best argument of all is empirical: the test program I wrote to compute fractal Newton basins worked the first time I compiled it, something that virtually never happens to me with C or C++.

In this post, I’ll provide a rough overview of functional programming and F#. There are much better introductions out there, but I nonetheless wanted to write this as a way to help myself learn about functional programming. I also figure F# is new enough that many of the people who read this blog might have not yet heard of it, and any small additional exposure this great language gets is worth it. This is not meant to provide a tutorial that will bring you up to speed on F#, but is intended to give you enough of an idea about it that you can decide whether or not you want to learn more.

In a follow up article, I’ll step through a short program in F# which uses some of the example functions I define below to implement a parallel computation of some pretty fractals generated by running Newton’s method for polynomial roots in the complex plane. In a third post, I’ll talk about some of the libraries available to speed up F# development. Because of the functional nature of F#, libraries written for F# can do some pretty impressive things. For example, the fractal generator detailed in the next post uses a third-party library function that handles all the details of multithreaded task parallelization through the surprisingly simple use of higher-order functions. In fact, parallelizing the program required typing exactly nine characters.

Continue reading →