NB: The recent release of the F# CTP breaks much of this code. I will update this page as soon as I get a chance, but please be aware that if you copy the code in as-is, it will not work.
I think the best way to appreciate how efficient F# is, especially for numerical analysis, is to show an implementation of a short program. The following is a bare-bones application which computes the basins of attraction for a Newton fixed point iteration which finds the roots of a polynomial in the complex plane. This computation is threaded across all available processors, and is a stand alone (albeit absolutely minimal) Windows application. The entire program is less than 50 lines, a testament to F# with respect to numerics and the .NET framework with respect to the GUI.
Briefly, Newton’s method is an iterative way to solve for the zeros of nonlinear functions. You start with an initial guess, and based on the local slope of the function, you make a refined guess for the root by following the slope all the way to zero. Unless the function really is a line this guess will be wrong, of course, but hopefully a little more accurate than where you started. If you start close enough to a root, repeated applications of the approximation will end up converging to the correct answer to arbitrary precision. If you start far away from one, however, you could end up at a root far away from your starting point, or you might never converge. It turns out that the map of where you end up as a function of where you start is a fractal, and a rather beautiful one for many equations. Below is a screen shot of the final program. Visible in the task manager is the nearly full usage of both cores of the processor during the render. (Click for a bigger version.)
The program below will iterate through up to 32 steps of Newton’s method on an arbitrary polynomial, starting at a grid of points in the complex plane. It shades each point based on the location of the final root found, with the hue determined by which root is converged to and with the brightness determined by how many steps were required. I’ll go through most of the functions, explaining each and pointing out how functional programming techniques are used. I do not claim this program is a highly efficient implementation! The main point was to illustrate several aspects of F#. It is however, pretty fast and makes use of multiple threads. In fact, the ease with which this program was parallelized is one of the main points I am trying to illustrate, and is made possible by the immutability of data in F# (and the Flying Frog Numerics library, a review of the which will be the subject of my final post on F#).
Below I’ve listed segments of code followed by brief explanations of each.
Â
// program to plot newton basins for a polynomial in the complex plane #light
// Load libraries #r @"C:Program FilesFlyingFrogflyingfrog.numerics.dll"
// open some namespaces open System open Drawing open Windows.Forms open Math open FlyingFrog
This is just boring namespace and library loading code. The #light syntax allows us to use abbreviated notation for many F# constructs, and seems to be the common usage. For example, it lets you forget about most end of line indicators. It kind of makes me wonder why they don’t just make #light the default and force you to use #heavy when you don’t want it, though I suppose the way language development works, that ship has sailed into the waters of backwards compatibility. The cost for the light syntax is that whitespace becomes significant, and you must indent your code correctly for the compiler to know what’s up. On the whole, this saves typing and makes for more readable code so I’ll stick with the #light syntax. Frankly, I’ve never actually seen anybody not use the light syntax.
Â
// tail recursive auxilary function for polynomial evaluation let rec polyval_aux (ps:float list) (x:Complex) (xpow:Complex) (accum:Complex) = match ps with | [] -> accum | c::psrest -> polyval_aux psrest x (x * xpow) (accum + (c $* xpow))
// evaluate polynomial with coefficients given by ps at x // the highest order coefficient is last let polyval ps x = polyval_aux ps x (Complex.Create (1.,0.)) (Complex.Create (0.,0.))
This is the recursive polynomial evaluation function that I spoke about in the previous post. The first function does all the work, and the second is just a wrapper that provides for a simpler call. (The use of recursion and pattern matching makes for a very simple imlementation, but for very large polynomials there are much more efficient ways to implement this that minimize the number of multiply operations.) The pattern matching facility of F# not only allows for a easy way to think about the control code (the two cases being those with empty lists and those with at least one entry) but it also simultaneously creates local variables (the first element “c” and the remaining elements in “psrest”) to be used within the second case. This is perhaps one of the most elegant aspects of F#: if you need to bother to specify a certain pattern of elements as a special case, then it’s likely you’ll want to use the specific instances of those elements. You thus specify your local variables at the same time that you specify your control code. Very elegent, useful and eminently readable. Pattern matching is by far my favorite aspect of F#.
Â
let polyderiv (ps:float list) =
match ps with
| [] -> []
| lowcoef::pshigh ->
List.mapi (fun k pcoef -> float (k+1) * pcoef) pshigh
Since Newton’s method needs the derivative of a function, it will be handy to have a function which takes a polynomial and computes its derivative (which is just another polynomial). As with the previous functions, this takes a polynomial expressed as a list of coefficients and outputs another list of coefficients. (This function is also explained in better detail in the previous post.) The main part of this function illustrates the use of the higher order function List.mapi, which iterates over a list, applying a function to each element (presuming a nonempty list). The function here is defined anonymously, using the fun keyword. Another nice aspect of F#’s pattern matching is that the compiler ensures you cover all corner cases. In this case, the compiler will consider it a syntax error if you don’t include the [] case.
Â
let maxcount = 32 // how many iterations before we give up on convergence
let rec fixed_point_count_aux f k (x : Complex) =
let f_x = f x // evaluate function
if ((f_x = x) || (k > (maxcount - 1))) then
(x,k)
else
fixed_point_count_aux f (k+1) f_x
let fixed_point_count f (x : Complex) = fixed_point_count_aux f 1 x
This set of functions simply iterates a function on a complex number, feeding the output back into the input, until either a fixed point is reached (to machine precisions) or maxcount iterations are completed. Additionally, a counter is kept of the total iterations. Naturally, the iteration is handled by a recursive function which starts by computing the given function on the current complex number. It then checks if the output of the function differs from the input or if the number of iterations (k) has exceeded maxcount. If so, it returns a “tuple” consisting of the final value and the iteration count. Otherwise, it calls itself with the updated complex number and the incremented iteration count. The second function is a wrapper for the first, which simply handles calling the auxiliary function with an initial iteration count of one.
Notice that we can define the fixed point iteration code completely generally and without knowledge of the fact that we’re going to be using it with Newton iterations. (In fact, if this weren’t such a simple implementation, it could be made into a library function, complete hiding all the details.) All we need to do now is supply the function “f” to be used, which we do below. Notice how much encapsulation is possible with functional programming without having to use a single object.
Â
let newton_iter f df (x : Complex) = // compute derivative at x let (dfx : Complex) = df x // if the derivate is finite, compute step if (dfx.Magnitude = 0.) then x else x - (f x)/(df x)
let newton_fixed_point_fun p = newton_iter (polyval p) (polyval (polyderiv p))
The first function above performs a general Newton iteration given a function “f” whose root we seek, given a function “df” which computes its derivate, and a starting guess “x” given as a complex number. For convenience, we also define a function which takes a polynomial and uses a curried version of newton_iter to return a function which takes a complex number and performs a Newton iteration for that polynomial. If we repeatedly apply this function to an approximate guess for a root, it will converge to the exact root. The newton_fixed_point_fun routine takes care of generating the derivative function needed, by using our polyderiv function.
Â
// compute display color from fixed point count result let result_to_color (x : Complex, k : int) = let mag = float (maxcount - k) / (float maxcount) let angle = x.Phase let compg = int (255.*mag*(Math.Sin(angle)/2. + 0.5)) let compb = int (255.*mag*(Math.Sin(angle + 6.28/3.)/2. + 0.5)) let compr = int (255.*mag*(Math.Sin(angle + 2.*6.28/3.)/2. + 0.5)) Color.FromArgb(compr, compg, compb)
Now we’ve got some utility functions to define. We need some way to display the results of each Newton solution at each point in the complex plane. The above function takes the output of fixed_point_count, which is a tuple consisting of the final point reached and the number of iterations required, and returns a Windows Color object. The details of this function aren’t very interesting, but the idea is that if a root is found from a given starting point, the pixel corresponding to that starting point will be colored based on which root it is, and with a brightness proportional to how quickly Newton’s method converged to it. If Newton’s method never converges, it will be black.
Â
let linspace (low, high) n =
let index_to_real k =
low + (high - low)*(float k)/(float (n - 1))
Array.map index_to_real [| 0 .. (n-1) |]
Another utility function. The way the computation will proceed is that each pixel in the output window will represent a value in the complex plane. We thus need a way to go from the pixel index to the number it refers to. This is done by linspace, which takes a low and high value, and the number of pixels n, and creates an array of n floats spanning from low to high. This kind of thing would usually have to be done with for loops in an imperative language like C. However, in F# it is done with the Array.map higher-order function, which applies a given function to an array. In my opinion, this is a much more conceptually satisfying way to do it, and one with far less potential for programmer errors.
This example also illustrates a very powerful aspect of functional programming: subfunctions. The index_to_real function which is passed to Array.map is defined inside linspace, and thus it can use all the local variables (and arguments) in linspace. This makes for much clearer usage in the map function.
Â
// main computational function to evaluate single line of fractal in parallel let compute_line f realparts imagpart = let cvals = Array.map (fun realpart -> Complex.Create(realpart,imagpart)) realparts Parallel.Array.map f cvals
The function compute_line is the heart of the program. It runs the Newton fixed point iterations for one single raster line of the fractal, distributing the computation over all available cores. It takes three arguments: the function “f,” a list of floats which represent the real part of the starting values at each pixel, and the single float which is the imaginary part of the starting values. (Since we’re doing a single horizontal line, the imaginary part stays the same.) The function “f” will be a curried version of the fixed_point_count function that we will define later, and it will return the aforementioned tuple which summarizes the results of the Newton iterations.
The first line of the function creates a list of complex values, representing the starting points of the Newton iterations. Then we simply call “f” on each complex value. Pretty simple, huh? What’s really cool is that by using Parallel.Array.map, a function in the Flying Frog Numerics Library, the computation is automatically threaded, distributing the computation over all available cores or processors. How can this be so simple? Why don’t we need to worry about thread safety? The reason this is possible is that every single variable used in the computation of the fractal is immutable. There’s no way for one thread to have side effects on the others. Now, in the case of this example program, the thread safety would be pretty trivial even in C#. However, the point here is that no matter how complex the algorithm, if you use immutable data structures in F# you will always be assured of thread safety. By simply typing the nine characters ‘Parallel.’ (and paying Flying Frog for the library, of course) you can turn a serial algorithm into a parallel one. This is a simple example, but there is a lot more coming along these lines. Microsoft, for all they get wrong, is really doing a good job staying on the ball with the seachange embodied by the move to many-core processors.
Â
// Create a bitmap the size of the rectangle and fill it using
// the fixed_point_count function "f" which generates a tuple from a complex
let format = Imaging.PixelFormat.Format24bppRgb
let make_bitmap_of f r_range i_range (r : Rectangle) =
let bitmap = new Bitmap(r.Width, r.Height, format)
let realparts = linspace r_range r.Width
let imagparts = linspace i_range r.Height
// aux function to compute line and write to bitmap
let do_line ki imagpart =
// run computation over raster line
let results = compute_line f realparts imagpart
// turn results into colors
let colors = Array.map result_to_color results
// set bitmap pixels to colors
Array.iteri (fun kr color -> bitmap.SetPixel(kr,ki,color)) colors
// iterate over the imaginary parts, computing each corresponding line
Array.iteri do_line imagparts
bitmap
The function make_bitmap_of comprises the main GUI routine, and creates a bitmap given a function “f”, the real and imaginary ranges over which to run the computation (expressed as tuples) and a rectangle representing the desired size of the bitmap. Nothing really interesting happens here, though. After some helper variable initialization and the creation of the blank Bitmap object, an auxiliary function do_line is defined that is designed to be used with Array.iteri. The function do_line will be run over a list of the imaginary parts representing each line of the fractal bitmap. It thus takes an index value and a float representing the imaginary part. It then runs compute_line and puts the results into a variable. Then, result_to_color is applied to each of the result tuples to generate a list of Color objects, which are then used to set each pixel color in the bitmap object.
Â
// Resize the form by replacing and rerendering the bitmap let resize f r_range i_range (b : Bitmap ref) (w : #Form) _ = b := make_bitmap_of f r_range i_range w.ClientRectangle; w.Invalidate()
// Paint the form by drawing the bitmap let paint (b : Bitmap ref) (v : #Form) (e : PaintEventArgs) = let r = e.ClipRectangle in e.Graphics.DrawImage(!b, r, r, GraphicsUnit.Pixel)
// Create a form that visualizes a bitmap that is rendered by the // function "f" let plot_newton f r_range i_range n = let form = new Form(Text="Newton Basins", Visible=true) in form.Size <- new Size(n, n); let r = form.ClientRectangle let bitmap = ref (new Bitmap(r.Width, r.Height, format)) form.Paint.Add(paint bitmap form); form.ResizeEnd.Add(resize f r_range i_range bitmap form); form.KeyDown.Add(fun e -> if e.KeyCode = Keys.Escape then form.Close()); form
This is just a bunch of boring .NET GUI code, which I’ll just leave as is for the sake of brevity. All I want to point out here is how relatively little of it is needed. This is not just a credit to .NET, but also to F# for its facile creation of callbacks. This code handles creating the window and setting callback functions to handing updating the fractal upon the window being resized, and to allow the user to quit by typing the escape key. Not much of a GUI, for sure, but it gets the job done. I think the .NET “form” object is the only mutable data structure in the entire program. (This snippet was essentially stolen wholesale from Jon Harrop.)
Â
// *** run example *** // create interesting polynomial let ps = [-1.0;0.01;-0.01;0.0;0.0;1.0] // create core function to run Newton's method let newton_test = fixed_point_count (newton_fixed_point_fun ps) // range to be used for both real and imagary parts to define plane let range = (-2.25,2.25) // create Windows form let form = plot_newton newton_test range range 256
#if COMPILED do Application.Run(form) #endif
Finally, the core application code. This is the stuff that would be inside the main() function in a C program, except that F# lets you just start writing code in a random file and figures (quite rightly) that if you bothered to write some code, you probably want it to run after you compile it. This generates the following fractal (click to see at high resolution):
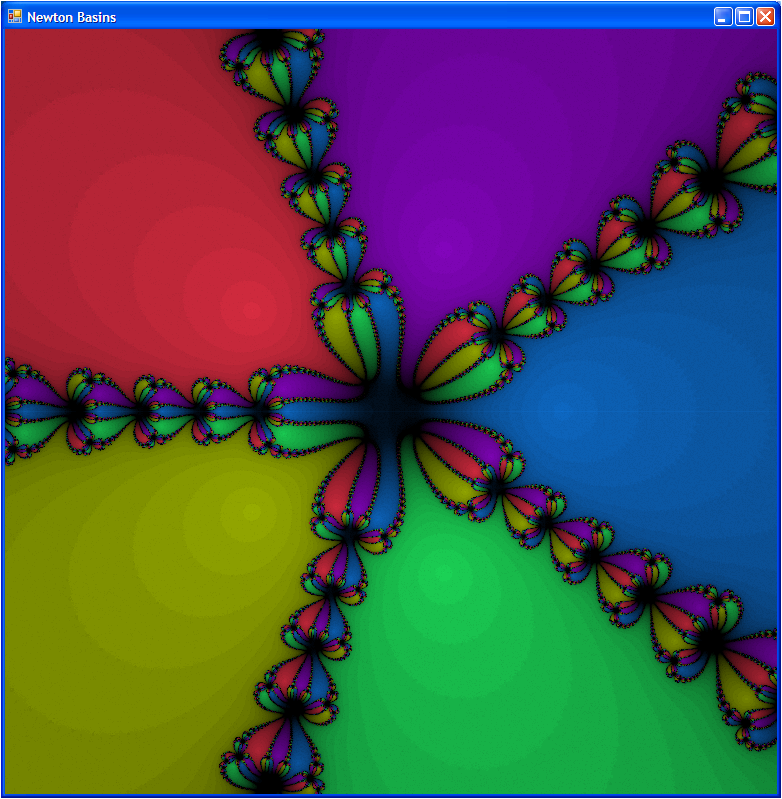
Newton basin fractal generated for a polynomial with five roots arrayed in a circle around the origin.
I hope this walk-through was at least somewhat useful in explaining some of the idioms of functional programming, and in particular those of F#. If anything requires better explanation, please send an e-mail or write a comment below. (Note: if you want to run this without the use of the FlyingFrog Numerics library, just delete the open command pertaining to it, and delete the “Parallel.” namespace prefix in the compute_line function.)
Pingback: valerio.net » Blog Archive » Long-awaited F# CTP Release!
Hi Jonathan, I am new to F# and was trying to learn about the language by following your notes on this page. However, when I sent the first few lines to the interpreter, I ran into some trouble on using complex types:
“error FS0039: The type ‘Complex’ is not defined. A construct with this name was found in FSharp.PowerPack.dll, which contains some modules and types that were implicitly referenced in some previous versions of F#. You may need to add an explicit reference to this DLL in order to compile this code.”
I took the hint in the error and tried to reference that dll:
#r @”C:\somePath\FSharp.PowerPack.dll”
however, when i resent the lines, I got this:
error FS0043: Method or object constructor ‘op_DollarMultiply’ not found.
I imagine I’ve just bungled up my setup in some uninteresting way but would appreciate any tips you might have.
Gratefully, Daniel
Daniel:
Sorry about that. You didn’t do anything wrong. The CTP release broke some of this code. In addition to the move of the Complex type, some operators were eliminated. I’ve fixed the code so that it works, but haven’t amended this post yet.
Hai,
Firstly i would like to apologise to all if this message is being interpreted as spam. Frankly, i have no business connection what soever with the owner of shaamtfractal.com (refer to as shaamtfractal). I would like to appeal to any person who knew the owner of the site to contact me personally or through this blog.
I have being following shaamtfractal since i stumbled upon it 3 weeks ago from a search engine. It seems that the fractal pattern is quite unique in the sense that it doesn’t match to any of the conventional formula known. I have failed to replicate it using any technique known (especially “Conflict Chamber 4”, “Turning Point 2” and most of it in the gallery). I am looking from the academic’s perspective and not from the artistic’s perspective because to me color & shade could easily be manipulated using a wide range of graphic tools.
Some of my academic collegue gave an opinion that the image could probably being produced from a high-end graphic software but they are amazed when i showed them the enlarge original’s image (7680 x 5760) because it exposed the very fine detail of the unique pattern not found in others fractal pattern. “Medussa Belt” clearly show a grow-like pattern.
I have tried in vain to get more details regarding the formula used from the site’s owner but the reply is that it is an industrial secret.
BTW, i am not trying to steal any formula from the site owner but just trying to get some clue regarding the formula & technique used to produce the said images and hoping that fractal theory could made a significant leap forward.
regards,
Fractal John Doe
-Fractal Math for civilisation advancement.
Thank you for sharing this information. I found your article very interesting, I tried to find out more by searching on the internet but I have not found … Can you please give me some websites that also speaks about the subject of your post?
Henry
I think you can find some information on wikipedia,
Check this webpage : http://en.wikipedia.org/wiki/Newton_fractal
there is an interesting page about the subject on this site mathworld.wolfram.com/NewtonsMethod.html
Interesting method. But one still should be aware of smaller vehicles, especially bicycles.
Pingback: Java Schools and the Desire to Know Everything « Dustin's Blog
The Visual F# CTP code,just learn it,and thanks
Pingback: F# Samples « Updates from a continuous developer
Pingback: F# in ASP.NET, mathematics and testing - Gunnar Peipman's ASP.NET blog
Well, great post, thanks. I love to read bicycles race posts and articles, thanks for sharing.
Excellent content, thanks for the input.
It’s interesting how fractals came about and the benefit they have given us in the computer design community. Without fractals we wouldn’t have the graphics we do today.
I Like to read about light oil.Got your page on Friday.Your Post Functional Programming and F#: Newton Basin Fractal Example Code | Jonathan Birge is really Nice.Thanks.
Man…I love Fractals!
Greetings I live in Washington, District of Columbia. I had to stop and comment on your blog. Thanks for sharing your site with us.
Hello Webmaster (Admin) This is great article. ? found your site on google.com And I love your blog if you have a new blog plzzz tell me. Thank you very much
I always emailed this weblog post page to all my friends, as
if like to read it next my contacts will too.
I constantly emailed this web site post page to all my contacts, since if like to read it afterward my friends will too.
SEO and social media has taken over everything we do online as marketers, I like the way you share with the community and through this you will gain more popularity.
We are a bunch of volunteers and opening a brand new scheme in our
community. Your website offered us with useful info
to work on. You have performed an impressive job and our
whole group shall be thankful to you.
This is my first time go to see at here and i am truly happy to read all at one place.