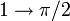From Yossi Farjoun's Homepage
hello
General
| Instructor
|
Yossi Farjoun, yfarjoun@math.mit.edu
|
| Grader
|
Stav Braun, sbraun@mit.edu
|
| Prerequisites
|
18.03 or 18.034
|
| Textbook
|
Numerical Analysis, Burden and Faires however, it is not required. Do not feel obliged to buy this book.
|
| Reader
|
This reader is a work-in-progress reader, please let me know of any typos/corrections etc.
|
| Location
|
TR 11-12:30 in 2-135
|
| Office hours
|
2-334 Tuesdays 4-5pm (but will go on longer for those who came on time and need more time)
|
| Phone (office)
|
(617) 253 7775
|
| Website (this one!)
|
http://scripts.mit.edu/~yfarjoun/homepage/index.php?title=18.330_Numerical_Analysis
|
Grades
The course will have written assignments, programming assignments, quizzes, mid-terms and a final. The grade will be determined by averaging:
- 10% Quizzes (about 5 throughout the semester)
- 10% Written H/W (about 10 total) No late submissions, grade is based on best 70%
- 25% Programming H/W (about 6 total) Must submit all but 1 to pass course
- 15% Each of 2 midterms
- 25% Final
Syllabus
- Calculus Review
- Iterative solutions of algebraic equations
- Chord method
- Secant method
- Newton's method
- Enough Linear Algebra for our needs
- Solution of triangular systems
- LU decomposition of tridiagonal matrices
- Solution of non-linear ODE
- Numerical Interpolation
- Numerical Integration
- Trapezoidal Rule
- Simpson's Method
- Numerical Solutions to PDE (Introduction)
Course Progress
| 2.3.2009
|
Calculus review. Continuous functions, Differential functions
|
| 2.5.2009
|
More Calculus review. We talked about derivatives and integrals, Mean Value Theorem: Fundamental Theorem of Calculus. Integration by Parts. Substitution.
|
| 2.10.2009
|
Calculus Review: Taylor series, O(h) notation. Examples.
|
| 2.12.2009
|
One last Example for calculus review. Start Fixed Point Methods
|
| 2.17.2009
|
Tuesday is a Monday! see you Thursday (Office hours are held today...)
|
| 2.19.2009
|
Higher-order iteration. Root finding methods.
|
| 2.24.2009
|
Tridiagonal linear systems, Example, O(n) solution, use of high dimension Newton's method.
|
| 2.26.2009
|
Quiz 1, Polynomial Interpolation, Existence and Uniqueness, Lagrange Form, Newton Form, Divided Differences (just a taste)
|
| 3.5.2009
|
More about divided differences, Mid-Term review.
|
| 3.10.2009
|
Mid-Term I Happened.
|
| 3.12.2009
|
Splines, a Derivation using functional derivatives.
|
| 3.17.2009
|
Returned midterm. Example using splines. Started discussion on Inner Product Spaces.
|
| 3.19.2009
|
Continue inner product spaces.
|
| 3.31.2009
|
Orthogonal Functions
|
| 4.2.2008
|
Finish Orthogonal functions and start integration. (planned)
|
Written Homework given
Programing Assignments
Exams Scheduled
| Feb 26
|
Quiz 1
|
Root finding, Fixed Point methods
|
| Mar 10
|
Mid-Term 1
|
Series, Error estimates, Iterative sequences and fixed points, Newton's Method, Discretized Boundary Value Problems (Formulating), Tri-diagonal Systems, Polynomial Interpolation. Midterm I Review
|
| Apr 2
|
Quiz 2
|
Orthogonal projection, Inner product spaces. This quiz will not be an exact question out of the homework, but rather an easy question in the spirit of the homework.
|
| Apr 14
|
Mid-Term 2
|
Polynomial interpolation, Splines, Orthogonal projection and inner-product spaces, and, of-course, everything else we have learned so far (not kidding!). If you wish, you can use problems on the midterm review to prepare. I will not provide solutions.
|
| Apr 21
|
Quiz 3
|
| May 18
|
Final 2
|
Here's a final review of questions of the type that are not in the mid-terms and quizzes: final review. I will not provide solutions. Expect 6 questions covering all of the material of the course, but more focused on the last part. Richardson Extrapolation, Trapezoidal and Simpson's rules, linear ODE's, numerical methods (Truncation Errors, stability of multi-step methods), Analysis of numerical methods for solving PDE (convergance and stability). The question on PDE from the review will be given verbatim in the final.
|
Links