Midterm I Review
From Yossi Farjoun's Homepage
To prepare for this midterm I can only remind you of the topics that we have covered and suggest ways in which you should prepare.
Methods:
- Make sure you know how to do all the homework problems given to date.
- Make sure you know the solution to the quiz.
- Read the relevant chapters in the reader.
- Discuss the material with your peers. I highly recommend this as a method of studying.
Material:
- You should totally grok the calculus review part of the course. While there will not be a question specifically asking about this part, you can be sure that many problems will have this material as required skill. Example problem:
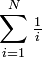 can be bounded using an an appropriate integral of a smooth function. Draw the relevant picture and find the bounds (plural because I want 2 bounds, one from above and one from below).
can be bounded using an an appropriate integral of a smooth function. Draw the relevant picture and find the bounds (plural because I want 2 bounds, one from above and one from below).
- Another example:
- Explain a derivation of the sum
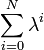 .
.
- Taylor Series, with/without remainder term, go over all our derivations of error for various expressions. Example for question: Calculate the error in the approximation
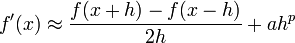 . (That is, find a and p.)
. (That is, find a and p.)
- Fixed point methods. You should understand the conditions for convergence and the methods of proof. You should remember the definition of order of convergence.
- Root finding. Understand the connection between fixed point methods and root finding methods. Example problem:
- In the derivation of Newton's Method we implicitly assume that the root is a regular root. If the root is not regular, so that
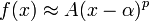 for some p > 1 and for x near α, the standard newtons method doesn't have second order convergence.
for some p > 1 and for x near α, the standard newtons method doesn't have second order convergence.
-
- Find the order of convergence of Newton's method in this case.
-
- Show that the second order convergence can be recovered by using
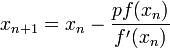
- Show that the second order convergence can be recovered by using
- The function cos(x) is approximated by an n-th order polynomial on n+1 nodes (equally distributed) between 0 and π / 2. Estimate the error of this interpolation.