18.330 Numerical Analysis (2008)
From Yossi Farjoun's Homepage
Contents |
Homework & Quizzes
Written Assignments
- Due Feb. 15
- Due Feb. 22
- Due Feb. 29
- Due Mar. 7
- Due Mar. 14
- Due Apr. 4
- Due Apr. 11
- Due Apr. 23
- Due May 5 This was updated Thursday
Bonus homework set for reviewing Projection method for solving BVP: Not Due
Computer Assignments
- Getting Started with Matlab Due Feb 20
- Iterative Root Finders Due Mar 5
- Polynomial Interpolation Due Mar 19
- LU Decomposition Apr 2
- Uses of LU Decomposition Apr 14
- Richardson Extrapolation Apr 25
- ODE Solvers May 7
Quizzes
- Calculus review, iterations and root finding, Feb 29
- Polynomial Interpolation and splines, Mar 21
- Orthogonal projection and inner products, Apr 7
- Numerical Integration and Richardson Extrapolation May 2
For help with learning Matlab I can offer some resources:
- A tiny sample of what Matlab can do
- Course notes from a Matlab course that I gave over IAP
- The official Mathworks user guide to Matlab
Mid-Terms and Final
- Mid-Term 1, on Mar 10 will consist of 3 problems:
- Series, in particular geometric series. Recall that we derived series for logarithms and trig functions and estimated errors by considering partial sums of series.
- Will consider an iteration of the form xn + 1 = g(xn). Be familiar with computations of
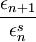 .
.
- Newton's method. Understand the ratio of successive error terms.
- (Error formula of polynomial interpolation...)
- Mid-term 2, on April 28 will cover 4 topics:
- Polynomial interpolation
- Splines
- Orthogonal projection
- Numerical integration
- Final, on Thursday, May 22, 2008 9am -- 12pm in room 4-231 will cover everything that we learned. in addition to the topics listed in the Midterms I might also ask on
- ODE solvers
- Numerical PDE solvers
I will be holding a Review Session on Friday (the 16th) starting at 2 and probably ending around 3:30. It will be in our regular classroom: 2-132.
Here are some review problems for Midterm 2
General
| Instructor | Yossi Farjoun |
| Grader | Sergiy Sidenko; Office hours: 2-588 Monday 4-5 |
| Prerequisites | 18.03 or 18.034 |
| Textbook | Numerical Analysis, Burden and Faires however, it is not required. Do not feel obliged to buy this book. |
| Reader | http://math.mit.edu/~yfarjoun/teaching/2008/18.330/reader.pdf is a Work-In-Progress reader. More about this Reader |
| Location | MWF 2-3pm in 2-132 |
| Office hours | 2-334 MW 3:30-5pm |
| Website | http://scripts.mit.edu/~yfarjoun/homepage/index.php?title=18.330_Numerical_Analysis |
Grades
The course will have written assignments, programming assignments, quizzes, mid-terms and a final. The grade will be determined by averaging:
- 10% Quizzes (about 5 throughout the semester)
- 10% Written H/W (about 10 total) No late submissions, grade is based on best 70%
- 25% Programming H/W (about 6 total) Must submit all but 1 to pass course
- 15% Each of 2 midterms (The first one is scheduled for Mar 10, 2008) Midterm 1 is "protected" by Midterm 2, and Midterm 2 by the final
- 25% Final
Syllabus
- Calculus Review
- Iterative solutions of algebraic equations
- Chord method
- Secant method
- Newton's method
- Enough Linear Algebra for our needs
- Solution of triangular systems
- LU decomposition of tri-diagonal matrixes
- Solution of non-linear ODE
- Numerical Interpolation
- Polynomial
- Spline
- Numerical Integration
- Trapezoidal Rule
- Simpson's Method
- Numerical Solutions to PDE (Introduction)